Ֆունկցիան մաթեմատիկայում, երկու բազմությունների տարրերի միջև համապատասխանության կանոն է, ըստ որի առաջինի յուրաքանչյուր տարր համապատասխանում է երկրորդ բազմության մեկ և միայն մեկ տարրին։
Ֆունկցիայի մաթեմատիկական հասկացությունն արտահայտում է ինտուիտիվ գաղափար այն մասին, թե ինչպես է մի մեծությունն ամբողջությամբ որոշում մեկ այլ մեծության արժեքը։ Այսպիսով {\displaystyle x}

Պատմություն
«Ֆունկցիա» տերմինը (մի փոքր ավելի նեղ իմաստով) առաջին անգամ օգտագործել է Լայբնիցը (1692 թվական)։ Իր հերթին Յոհան Բեռնուլին Լայբնիցին ուղղված նամակում այս տերմինին ավելի մոտ իմաստ է տվել ժամանակակցին։ Սկզբում ֆունկցիա հասկացությունը չէր տարբերվում վերլուծական ներկայացման հասկացությունից։ Հետագայում հայտնվեց ֆունկցիայի սահմանումը, որը տրվել է Էյլերի (1751), այնուհետև Լակրուայի (1806) կողմից, գրեթե ժամանակակից ձևով։ Վերջապես, ֆունկցիայի ընդհանուր սահմանումը (ժամանակակից ձևով, բայց միայն թվային ֆունկցիաների համար) տրվել է Լոբաչևսկու (1834) և Դիրիխլեի (1837) կողմից։ 19-րդ դարի վերջում ֆունկցիա հասկացությունը գերազանցել էր թվային համակարգերի շրջանակը։ Սկզբում ֆունկցիա հասկացությունը տարածվեց վեկտորային ֆունկցիաների վրա, Ֆրեգեն շուտով ներկայացրեց տրամաբանական ֆունկցիաները (1879 թվական), իսկ բազմությունների տեսության հայտնվելուց հետո Դեդեկինդը (1887 թվական) և Պեանոն (1911 թվական) ձևակերպեցին ժամանակակից ունիվերսալ սահմանումը։
Մոնոտոն ֆունկցիաներ
y=f(x) ֆունկցիան կոչվում է X բազմությունում աճող, եթե ցանկացած x1 և x2 թվերի համար X բազմությունից x1<x2 անհավասարությունից հետևում է, որ f(x1)<f(x2) y=f(x) ֆունկցիան կոչվում է X բազմությունում նվազող, եթե ցանկացած x1 և x2 թվերի համար X բազմությունից x1<x2 անհավասարությունից հետևում է, որ [5;7]
Այլ բառերով՝ ֆունկցիան աճում է, եթե արգումենտի մեծ արժեքին համապատասխանում է ֆունկցիայի մեծ արժեքը, և ֆունկցիան նվազում է, եթե արգումենտի մեծ արժեքին համապատասխանում է ֆունկցիայի փոքր արժեքը:
Թվային ֆունկցիա, նրա որոշման տիրույթն ու արժեքների բազմությունը
Դիցուք X-ը որևէ թվային բազմություն է: Եթե այդ բազմության յուրաքանչյուր x թվի որոշակի f օրենքով համապատասխանության մեջ է դրվում ճիշտ մեկ y թիվ, ապա ասում են, որ X բազմության վրա տրված է y=f(x) ֆունկցիան:
X բազմությունը անվանում են y=f(x) ֆունկցիայի որոշման տիրույթ:x-ը անվանում են անկախ փոփոխական կամ արգումենտ, իսկ նրան համապատասխանող y թիվը՝ կախյալ փոփոխական կամ ֆունկցիայի արժեք x կետում: f(x) ֆունկցիայի բոլոր արժեքների բազմությունն անվանում են y=f(x) ֆունկցիայի արժեքների բազմություն:
f ֆունկցիայի որոշման տիրույթը ընդունված է նշանակել D(f)-ով, իսկ արժեքների տիրույթը՝ E(f)-ով: Սահմանումից հետևում է, որ ֆունկցիայի տրման համար պետք է նկարագրված լինի f կանոնը` իր որոշման տիրույթի հետ միասին: Սակայն հաճախ, երբ ֆունկցիան տրված է լինում անալիտիկ՝ բանաձևով, որոշման տիրույթը բացահայտ չի նշվում:
Այդ դեպքերում ֆունկցիայի որոշման տիրույթը անկախ փոփոխականի բոլոր այն արժեքների բազմությունն է, որոնցից յուրաքանչյուրի համար ֆունկցիան ընդունում է իրական արժեքներ:
f(x)=2x+1/1−x2 բանաձևով տրված ֆունկցիայի որոշման տիրույթը բոլոր իրական թվերի բազմությունն է, բացի1 և −1թվերից, այսինքն՝ D(f)=(−∞;−1)∪(−1;1)∪(1;+∞)
Վերհիշենք նաև, որ y=f(x) ֆունկցիայի գրաֆիկ անվանում են xOy կոորդինատային հարթության վրա (x;f(x)) տեսքի բոլոր կետերի բազմությունը, որտեղ x-ը որոշման տիրույթի կամայական կետ է:
Ֆունկցիայի արժեքների բազմությունը գտնելու խնդիրը ընդհանուր դեպքում բարդ է:Այդ խնդիրը լուծելու համար հարմար է կառուցել ֆունկցիայի գրաֆիկը և տեսնել, թե ի՞նչ բազմություն է իրենից ներկայացնում գրաֆիկի պրոյեկցիան օրդինատների առանցքի վրա:
Գծային ֆունկցիան և նրա գրաֆիկը
y=kx+b տեսքի ֆունկցիան, որտեղ k-ն և b-ն տրված թվեր են, անվանում են գծային ֆունկցիա:
y=kx+b ֆունկցիան իմաստ ունի ցանկացած x-ի համար՝ ունենալով x-ի ցանկացած արժեք, բանաձևի օգնությամբ, կարելի է հաշվել y-ի համապատասխան արժեքը: Սա նշանակում է, որ y=kx+b ֆունկցիայի որոշման տիրույթը բոլոր իրական թվերի բազմությունն է:
Եթե b=0, ապա ստանում ենք y=kx ուղիղ համեմատականության ֆունկցիան:
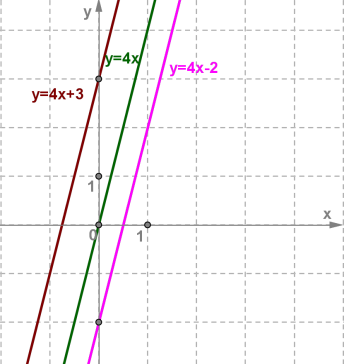
Կառուցենք y=4x+3 ֆունկցիայի գրաֆիկը: Նախ կառուցենք y=4x ֆունկցիայի գրաֆիկը: Արդեն գիտենք, որ դա (0;0) կետով անցնող ուղիղ գիծ է:
Համեմատելով y=4x+3 և y=4x բանաձևերը՝ նկատում ենք, որ նույն x-ի համար y=4x+3 ֆունկցիայի y-ը 3-ով մեծ է y=4x ֆունկցիայի y-ից: Սա նշանակում է, որ եթե (x;y)−ը y=4x ֆունկցիայի գրաֆիկի կետ է, ապա y=4x+3 գծային ֆունկցիայի գրաֆիկի համապատասխան կետը կունենա (x;y+3) տեսքը:
Հետևաբար, գրաֆիկը կառուցելու համար կարելի է վարվել հետևյալ կերպ:
Տեղափոխենք y=4x ֆունկցիայի գրաֆիկը դեպի վեր 3 միավորով՝ կստանանք y=4x+3 ֆունկցիայի գրաֆիկը: Այսպիսով՝
y=kx+b գծային ֆունկցիայի գրաֆիկը ուղիղ գիծ է, որը զուգահեռ է y=kx ֆունկցիայի գրաֆիկին և ստացվում է դրանից զուգահեռ տեղափոխությամբ b միավորով:
y=kx+b գծային ֆունկցիայի k թիվը անվանում են անկյունային գործակից: Այսպիսով՝ նույն անկյունային գործակցով ուղիղները զուգահեռ են:
Եթե k>0, ապա y=kx+b ուղիղը x-երի առանցքի դրական ուղղության հետ կազմում է սուր անկյուն, եթե k<0, ապա այդ անկյունը բութ է:
Եթե y=kx+b բանաձևում տեղադրենք x=0, ապա կստանանք՝ y=b: Այսպիսով՝ (0;b) կետը միշտ պատկանում է y=kx+b գծային ֆունկցիայի գրաֆիկին, իսկ b թիվը ցույց է տալիս, թե որ կետում է ուղիղը հատում y-ների առանցքը:
Դիտարկենք ֆունկցիաների օրինակներ:
Օրինակ 1: Մայրուղու վրա գտնվում են A և երկու B կետերը, որոնց միջակա հեռավորությունը 20կմ է: Մոտոցիկլավարը դուրս եկավ B կետից և 50կմ/ժ արագությամբ շարժվեց A կետի հակառակ ուղղությամբ: t ժամում մոտոցիկլավարը կանցնի 50t կմ և A-ից հեռու կլինի (50t + 20) կմ: Եթե s տառով նշանակենք A կետից մոտոցիկլավարի հեռավորությունը (կիլոմետրերով), ապա այդ հեռավորության կախվածությունը շարժման ժամանակամիջոցից կարելի է արտահայտել հետևյալ բանաձևով.
s = 50t + 20, որտեղ t ≥ 0:
Օրինակ 2: Աշակերտը գնել է 30 դրամանոց տետրեր և 150 դրամանոց մի գրիչ: Վճարը կախված է տետրերի թվից: Գնված տետրերի թիվը նշանակենք x, իսկ վճարը (դրամներով) y տառով:
Կստանանք.y = 30x + 150, որտեղ x-ը բնական թիվ է:
Երկու օրինակներում էլ մենք հանդիպեցինք այնպիսի ֆունկցիաների, որոնք տրվում են y = kx + b տեսքի բանաձևերով, որտեղ x-ը անկախ փոփոխական է, k-ն և b-ն թվեր են: Այդպիսի ֆունկցիաները կոչվում են գծային:
Սահմանափակ ֆունկցիաներ
y=f(x) ֆունկցիան անվանում են ներքևից սահմանափակ X⊂D(f) բազմության վրա, եթե գոյություն ունի այնպիսի m թիվ, որ ցանկացած x∈X արգումենտի համար տեղի ունի f(x)≥m անհավասարությունը:
y=f(x) ֆունկցիան անվանում են վերևից սահմանափակ X⊂D(f) բազմության վրա, եթե գոյություն ունի այնպիսի M թիվ, որ ցանկացած x∈X արգումենտի համար տեղի ունի f(x)≤M անհավասարությունը:
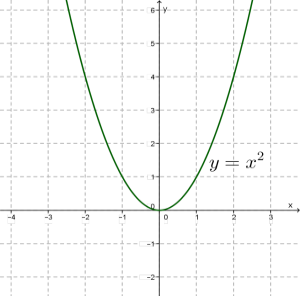
Օրինակա) y=x2 ֆունկցիան սահմանափակ է ներքևից ամբողջ թվային առանցքի վրա, օրինակ զրոյով, քանի որ x2≥0 անհավասարությունը տեղի ունի ցանկացած իրական թվի համար:
բ) y=−x2 ֆունկցիան սահմանափակ է վերևից ամբողջ թվային առանցքի վրա, օրինակ զրոյով, քանի որ −x2≤0 անհավասարությունը տեղի ունի ցանկացած իրական թվի համար:
y=f(x) ֆունկցիան անվանում են սահմանափակ X⊂D(f) բազմության վրա, եթե այն սահմանափակ է և՛ ներքևից և՛ վերևից, այսինքն գոյություն ունեն այնպիսի m և M թվեր, որ ցանկացած x∈X արգումենտի համար տեղի ունի m≤f(x)≤M կրկնակի անհավասարությունը:
Ապացուցել ֆունկցիայի սահմանափակությունը` նշանակում է գտնել m և M թվերը:
Օրինակա) y=x3 ֆունկցիան սահմանափակ է x∈[1;2] բազմության վրա, քանի որ 1≤x3≤8 անհավասարությունը տեղի ունի ցանկացած x∈[1;2] արգումենտի համար:
բ) Նույն y=x3 ֆունկցիան [0;+∞) բազմության վրա ներքևից սահմանափակ է զրոյով՝ x3≥0, x∈[0;+∞), սակայն վերևից սահմանափակ չէ, քանի որ այն ընդունում է ցանկացած դրական թվից մեծ արժեքներ:
Բերենք սահմանափակ ֆունկցիայի ևս մեկ սահմանում, որը համարժեք է արդեն տրված սահմանմանը:
y=f(x) ֆունկցիան անվանում են սահմանափակ X⊂D(f) բազմության վրա, եթե գոյություն ունի այնպիսի A թիվ, որ ցանկացած x∈X արգումենտի համար տեղի ունի |f(x)|≤A անհավասարությունը:

Պարբերական ֆունկցիաներ
Ասում են, որ y=f(x), x∈X ֆունկցիան ունի T պարբերություն, եթե կամայական x∈X արգումենտի համար տեղի ունեն հետևյալ հավասարությունները՝ f(x−T)=f(x)=f(x+T)
Զրոյից տարբեր T պարբերություն ունեցող ֆունկցիան կոչվում է պարբերական:
Եթե y=f(x), x∈X ֆունկցիան ունի T պարբերություն, ապա T-ին պատիկ ցանկացած թիվ ևս y=f(x) ֆունկցիայի պարբերությունն է:
Պարբերական ֆունկցիան ունի անվերջ թվով պարբերություններ:
Մեծամասամբ դրանց մեջ լինում է ամենափոքր դրական պարբերությունը:
Եթե պարբերական ֆունկցիան ունի փոքրագույն դրական պարբերություն, ապա այն անվանում են հիմնական պարբերություն:
Պարբերական ֆունկցիայի լավ օրինակներ են y=sinx և y=cosx եռանկյունաչափական ֆունկցիաները: Դրանց պարբերությունը հավասար է 2π
y=tgx և y=ctgx ֆունկցիաները ևս պարբերական են՝ π պարբերությամբ:
Նույնաբար հաստատուն y=const ֆունկցիան ևս պարբերական է: Նրա համար ցանկացածT≠0 թիվ պարբերություն է:

Եռանկյունաչափական ֆունկցիաների սահմանումը
Միավոր շրջանագծի վրա վերցնենք B(x;y) կետը և դիտարկենք OBD ուղղանկյուն եռանկյունը:
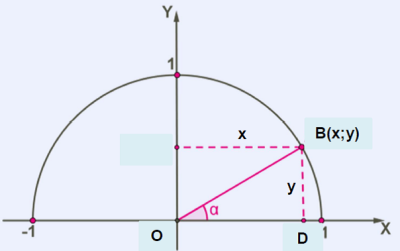
Երկրաչափության դասընթացից գիտենք, որ
sinα=BD/OB=y/1; cosα=OD/OB=x/1
tgα=BD/OD=y/x; ctgα=OD/BD=x/y
Այսպիսով՝ B(cosα;sinα)
1. sinα կոչվում է B կետի y կոորդինատը՝ օրդինատը:
2. cosα կոչվում է B կետի x կոորդինատը՝ աբսցիսը:
3. tgα կոչվում է B կետի օրդինատի հարաբերությունը աբսցիսին:
4. ctgα կոչվում է B կետի աբսցիսի հարաբերությունը օրդինատին
Սինուսը, կոսինուսը, տանգենսը և կոտանգենսը կոչվում են եռանկյունաչափական ֆունկցիաներ:
Միավոր շրջանագծի կամայական B(x;y) կետի կոորդինատների համար տեղի ունեն հետևյալ անհավասարությունները՝ −1≤x≤1;−1≤y≤1: Հետևաբար, ցանկացած α անկյան սինուսը և կոսինուսը բավարարում են−1≤cosα≤1;−1≤sinα≤1 անհավասարություններին:
Քանի որ միավոր շրջանագծի վրայով դրական կամ բացասական ուղղություններով լրիվ պտույտներ կատարելիս կետի դիրքը չի փոխվում, ապա՝ sin(α±2π)=sinα;cos(α±2π)=cosαtg(α±2π)=tgα;ctg(α±2π)=ctgα
| α k∈Z | 2πk | π2+2πk | π+2πk | 3π2+2πk |
| sinα | 0 | 1 | 0 | −1 |
| cosα | 1 | 0 | −1 | 0 |
| tgα | 0 | որոշված չէ | 0 | որոշված չէ |
| ctgα | որոշված չէ | 0 | որոշված չէ | 0 |